publications | Manuel Soriano Trigueros

2025

preprint
The Depth Poset under Transpositions in the Filter

Herbert Edelsbrunner, Michał Lipiński, Marian Mrozek, and Fedor Zimin Manuel Soriano-Trigueros

arXiv, Nov 2025

Abs arXiv Bib

The depth poset of a filtered Lefschetz complex reflects the dependencies between the cancellations of different shallow birth-death pairs. Using the fast algorithms for computing the depth poset in the present work and for updating the persistence diagram under transpositions (Vineyard persistence), we give a complete case analysis of how transpositions of cells in the filter affect the depth poset. In addition, we present statistics on the depth poset for random point data and its sensitivity to the transpositions that occur in random straight-line homotopies.
@article{transpositions_depth, title = {The Depth Poset under Transpositions in the Filter}, journal = {arXiv}, volume = {}, pages = {}, year = {2025}, month = nov, issn = {arXiv:2511.21961}, doi = {}, author = {Edelsbrunner, Herbert and Lipiński, Michał and Mrozek, Marian and Manuel Soriano-Trigueros, Fedor Zimin}, keywords = {vineyards, persistent homology, depth poset, shallow pairs}, }
proceeding
Additive partial matchings for persistent homology

Rocio Gonzalez-Diaz, Manuel Soriano-Trigueros, and Álvaro Torras-Casas

ISSAC ’25: Proceedings of the 2025 International Symposium on Symbolic and Algebraic Computation, Nov 2025

Abs Bib HTML

Persistence modules (defined as a sequence of vector spaces and linear maps between them) are a key tool in topological data analysis. They are easy to interpret and fast to compute. However, when considering persistence maps (i.e. maps between persistence modules), these properties are lost. We propose a new invariant for persistence maps consisting of a partial matching such that: it is easy to interpret, it is more discriminative than the image of the persistence map, and can be calculated with cubical complexity.
@article{ISSAC2025, title = {Additive partial matchings for persistent homology}, journal = {ISSAC '25: Proceedings of the 2025 International Symposium on Symbolic and Algebraic Computation}, volume = {}, pages = {188--196}, year = {2025}, month = nov, author = {Gonzalez-Diaz, Rocio and Soriano-Trigueros, Manuel and Torras-Casas, Álvaro}, doi = {10.1145/3747199.3747561}, }
preprint
Conley-Morse Persistence Barcode: a Homological Signature of a Combinatorial Bifurcation

Tamal K. Dey, Michał Lipiński, and Manuel Soriano-Trigueros

arXiv, Apr 2025

Abs arXiv Bib

Bifurcation is one of the major topics in the theory of dynamical systems. It characterizes the nature of qualitative changes in parametrized dynamical systems. In this work, we study combinatorial bifurcations within the framework of combinatorial multivector field theory–a young but already well-established theory providing a combinatorial model for continuous-time dynamical systems (or simply, flows). We introduce Conley-Morse persistence barcode, a compact algebraic descriptor of combinatorial bifurcations. The barcode captures structural changes in a dynamical system at the level of Morse decompositions and provides a characterization of the nature of observed transitions in terms of the Conley index. The construction of Conley-Morse persistence barcode builds upon ideas from topological data analysis (TDA). Specifically, we consider a persistence module obtained from a zigzag filtration of topological pairs (formed by index pairs defining the Conley index) over a poset. Using gentle algebras, we prove that this module decomposes into simple intervals (bars) and compute them with algorithms from TDA known for processing zigzag filtrations.
@article{CMbarcode, title = {Conley-Morse Persistence Barcode: a Homological Signature of a Combinatorial Bifurcation}, journal = {arXiv}, volume = {}, pages = {}, year = {2025}, month = apr, issn = {arXiv:2504.17105 }, author = {Dey, Tamal K. and Lipiński, Michał and Soriano-Trigueros, Manuel}, keywords = {Combinatorial dynamical system, persistent homology, gentle algebra, block decomposition}, }

2024

preprint
The Poset of Cancellations in a Filtered Complex

Herbert Edelsbrunner, Michał Lipiński, Marian Mrozek, and Manuel Soriano-Trigueros

arXiv, Nov 2024

Abs arXiv Bib

Motivated by questions about simplification and topology optimization, we take a discrete approach toward the dependency of topology simplifying operations and the reachability of perfect Morse functions. Representing the function by a filter on a Lefschetz complex, and its (non-essential) topological features by the pairing of its cells via persistence, we simplify using combinatorially defined cancellations. The main new concept is the depth poset on these pairs, whose linear extensions are schedules of cancellations that trim the Lefschetz complex to its essential homology. One such linear extensions is the cancellation of the pairs in the order of their persistence. An algorithm that constructs the depth poset in two passes of standard matrix reduction is given and proven correct.
@article{depth_poset, title = {The Poset of Cancellations in a Filtered Complex}, journal = {arXiv}, volume = {}, pages = {}, year = {2024}, month = nov, issn = {arXiv:2311.14364}, doi = {}, author = {Edelsbrunner, Herbert and Lipiński, Michał and Mrozek, Marian and Soriano-Trigueros, Manuel}, keywords = {Lefschetz complexes, persistent homology, depth poset, shallow pairs}, }
preprint
Additive Partial Matchings Induced by Persistence Morphisms

Rocio Gonzalez-Diaz, Manuel Soriano-Trigueros, and Álvaro Torras-Casas

arXiv, Oct 2024

Abs arXiv Bib

Given a morphism of persistence modules (a.k.a. persistence morphism) f:V→U, we introduce a novel operator that determines a partial matching between the barcodes of V and U induced by f. We show that the proposed operator is additive with respect to the direct sum of persistence morphisms, and that it contains more information than fV and the rank invariant. We also illustrate some advantages of using our induced partial matching over the Bauer-Lesnick partial matching χf. Lastly, we provide a family of persistence morphisms that contain modules built from Morse filtrations, for which χf, the rank invariant and our proposed induced partial matching are equivalent.
@article{GONZALEZDIAZ2023ADDITIVE, title = {Additive Partial Matchings Induced by Persistence Morphisms}, journal = {arXiv}, volume = {}, pages = {}, year = {2024}, month = oct, issn = {arXiv:2006.11100}, doi = {}, author = {Gonzalez-Diaz, Rocio and Soriano-Trigueros, Manuel and Torras-Casas, Álvaro}, keywords = {Partial matchings, Persistence modules, Topological data analysis, Block functions}, }

2023

A Survey of Vectorization Methods in Topological Data Analysis

Dashti Ali, Aras Asaad, Maria-Jose Jimenez, Vidit Nanda, Eduardo Paluzo-Hidalgo, and Manuel Soriano-Trigueros

IEEE Transactions on Pattern Analysis and Machine Intelligence, Dec 2023

Abs arXiv Bib HTML

Attempts to incorporate topological information in supervised learning tasks have resulted in the creation of several techniques for vectorizing persistent homology barcodes. In this paper, we study thirteen such methods. Besides describing an organizational framework for these methods, we comprehensively benchmark them against three well-known classification tasks. Surprisingly, we discover that the best-performing method is a simple vectorization, which consists only of a few elementary summary statistics. Finally, we provide a convenient web application which has been designed to facilitate exploration and experimentation with various vectorization methods.
@article{10235748, author = {Ali, Dashti and Asaad, Aras and Jimenez, Maria-Jose and Nanda, Vidit and Paluzo-Hidalgo, Eduardo and Soriano-Trigueros, Manuel}, journal = {IEEE Transactions on Pattern Analysis and Machine Intelligence}, title = {A Survey of Vectorization Methods in Topological Data Analysis}, year = {2023}, month = dec, volume = {}, number = {}, pages = {1-14}, doi = {10.1109/TPAMI.2023.3308391}, }
Barcodes of Persistence Modules: from Summaries to Matchings

Manuel Soriano-Trigueros

Universidad de Sevilla. Thesis supervised by Rocío González-Díaz and María-José Jiménez, May 2023

Abs Bib HTML

During recent decades, the application of topology to data analysis has experienced a revolution due to persistent homology. Persistent homology and its barcode representation offer many advantages to data analysis, such as the stability of the results and the possibility of quantifying qualitative geometric and topological features. The aim of this thesis is to enrich the existing knowledge about persistent homology and barcodes from three different perspectives. Each of these perspectives has led to a publication that together constitute the core of this thesis. First, from a statistical perspective, we study the stability properties of persistent entropy, a variable used to compare barcodes. In addition, we propose a new barcode vectorization method based on persistent entropy, which is more suitable for machine learning than persistent entropy itself. Second, from an applied perspective, we use barcode summaries to study the geometric and topological features of 2D images of epithelial cells. Lastly, from the algebraic perspective, we study how we can induce a partial matching between barcodes from a morphism between persistence modules, the algebraic structure underlying persistent homology. This study has led to the definition of an operator for such morphisms, called the induced block function. Moreover, we study some of its theoretical properties, such as linearity with respect to direct sums, and provide an algorithm to compute it in polynomial time.
@article{barcode, title = {Barcodes of Persistence Modules: from Summaries to Matchings}, journal = {Universidad de Sevilla. Thesis supervised by Rocío González-Díaz and María-José Jiménez}, volume = {}, pages = {}, year = {2023}, month = may, issn = {}, doi = {}, author = {Soriano-Trigueros, Manuel}, keywords = {}, }

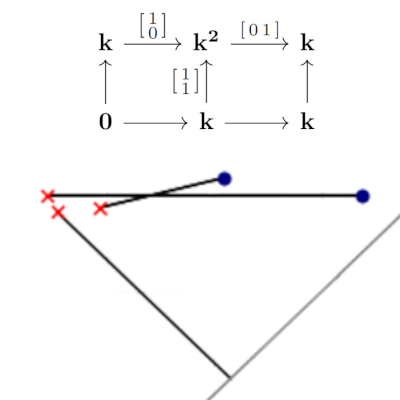Partial matchings induced by morphisms between persistence modules

Rocio Gonzalez-Diaz, Manuel Soriano-Trigueros, and Álvaro Torras-Casas

Computational Geometry, Feb 2023

Abs arXiv Bib HTML

We study how to obtain partial matchings using the block function Mf, induced by a morphism f between persistence modules. Mf is defined algebraically and is linear with respect to direct sums of morphisms. We study some interesting properties of Mf, and provide a way of obtaining Mf using matrix operations.

@article{GONZALEZDIAZ2023101985,
  title = {Partial matchings induced by morphisms between persistence modules},
  journal = {Computational Geometry},
  volume = {112},
  pages = {101985},
  year = {2023},
  month = feb,
  issn = {0925-7721},
  doi = {https://doi.org/10.1016/j.comgeo.2023.101985},
  author = {Gonzalez-Diaz, Rocio and Soriano-Trigueros, Manuel and Torras-Casas, Álvaro},
  keywords = {Partial matchings, Persistence modules, Topological data analysis, Block functions},
}

2022

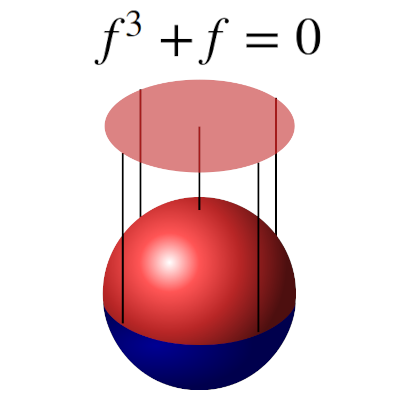Can trans-S-manifolds be defined from the Gray-Hervella classification for almost Hermitian manifolds?

Pablo Alegre, Luis M. Fernández, and Manuel Soriano-Trigueros

Annali di Matematica Pura ed Applicata (1923 -), Apr 2022

Abs Bib HTML

Recently, trans-S-manifolds have been defined as a wide class of metric f-manifolds which includes, for instance, f-Kenmotsu manifolds, S-manifolds and C-manifolds and generalize well-studied trans-Sasakian manifolds. The definition of trans-S-manifolds is formulated using the covariant derivative of the tensor f and although this formulation coincides with the characterization of trans-Sasakian manifolds in such a particular case, this latter type of manifolds were not initially defined in this way but using the Gray-Hervella classification of almost Hermitian manifolds. The aim of this paper is to study how (almost) trans-S-manifolds relate with the Gray-Hervella classification and to establish both similarities and differences with the trans-Sasakian case.
@article{Alegre2022, doi = {10.1007/s10231-022-01215-9}, year = {2022}, month = apr, publisher = {Springer Science and Business Media {LLC}}, volume = {201}, number = {6}, pages = {2691--2706}, author = {Alegre, Pablo and Fern{\'{a}}ndez, Luis M. and Soriano-Trigueros, Manuel}, title = {Can trans-S-manifolds be defined from the Gray-Hervella classification for almost Hermitian manifolds?}, journal = {Annali di Matematica Pura ed Applicata (1923 -)}, }

2021

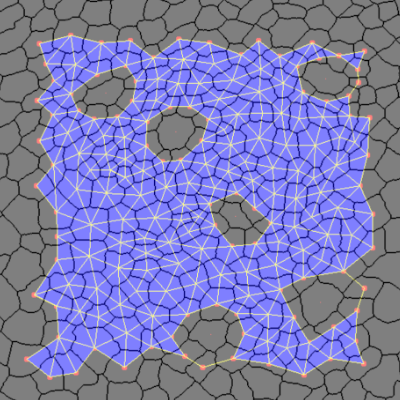Stable Topological Summaries for Analyzing the Organization of Cells in a Packed Tissue

Nieves Atienza, Maria-Jose Jimenez, and Manuel Soriano-Trigueros

Mathematics, Jul 2021

Abs arXiv Bib HTML

We use topological data analysis tools for studying the inner organization of cells in segmented images of epithelial tissues. More specifically, for each segmented image, we compute different persistence barcodes, which codify the lifetime of homology classes (persistent homology) along different filtrations (increasing nested sequences of simplicial complexes) that are built from the regions representing the cells in the tissue. We use a complete and well-grounded set of numerical variables over those persistence barcodes, also known as topological summaries. A novel combination of normalization methods for both the set of input segmented images and the produced barcodes allows for the proven stability results for those variables with respect to small changes in the input, as well as invariance to image scale. Our study provides new insights to this problem, such as a possible novel indicator for the development of the drosophila wing disc tissue or the importance of centroids’ distribution to differentiate some tissues from their CVT-path counterpart (a mathematical model of epithelia based on Voronoi diagrams). We also show how the use of topological summaries may improve the classification accuracy of epithelial images using a Random Forest algorithm.
@article{ATIENZA2021, title = {Stable Topological Summaries for Analyzing the Organization of Cells in a Packed Tissue}, volume = {9}, issn = {2227-7390}, doi = {http://dx.doi.org/10.3390/math9151723}, number = {15}, journal = {Mathematics}, publisher = {MDPI AG}, author = {Atienza, Nieves and Jimenez, Maria-Jose and Soriano-Trigueros, Manuel}, year = {2021}, month = jul, pages = {1723}, }

2020

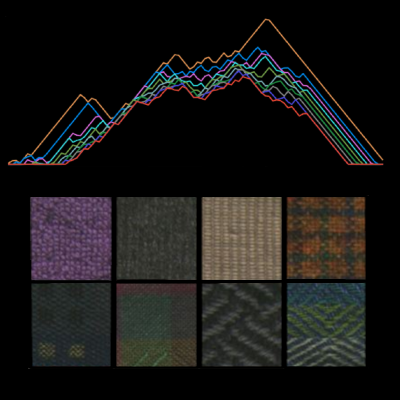
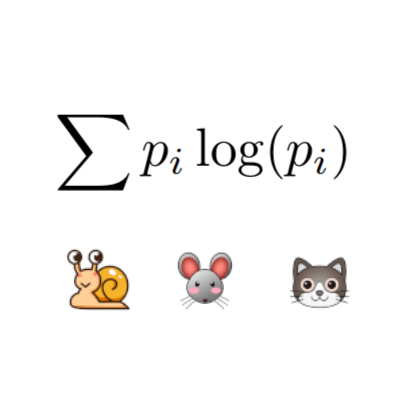On the stability of persistent entropy and new summary functions for topological data analysis

Nieves Atienza, Rocio Gonzalez-Diaz, and Manuel Soriano-Trigueros

Pattern Recognition, Nov 2020

Abs arXiv Bib HTML

Persistent homology and persistent entropy have recently become useful tools for patter recognition. In this paper, we find requirements under which persistent entropy is stable to small perturbations in the input data and scale invariant. In addition, we describe two new stable summary functions combining persistent entropy and the Betti curve. Finally, we use the previously defined summary functions in a material classification task to show their usefulness in machine learning and pattern recognition.
@article{ATIENZA2020107509, title = {On the stability of persistent entropy and new summary functions for topological data analysis}, journal = {Pattern Recognition}, volume = {107}, pages = {107509}, year = {2020}, month = nov, issn = {0031-3203}, doi = {https://doi.org/10.1016/j.patcog.2020.107509}, url = {https://www.sciencedirect.com/science/article/pii/S0031320320303125}, author = {Atienza, Nieves and Gonzalez-Diaz, Rocio and Soriano-Trigueros, Manuel}, keywords = {Persistent homology, Persistent entropy, Stability, Dimensionality reduction}, }