Vectorization methods

In Topological Data Analysis (TDA), the workflow used when using persistent homology is rather homogeneous, and can be summarized as follows:

1. We start with a data set, usually some finite metric space.
2. Then, a filtration is defined over such data set.
3. The persistent homology of the filtration is computed, to obtain a barcode.
4. Finally, barcodes are analyzed to extract the conclusions of our study. However, barcodes are not convinient for statistical tests and machine learning.

In particular, they lack of some of the properties that vector spaces have, like having an unique mean [MMH-2011]. For this reason, barcodes are usually send to a vector space (also denoted topological summaries) before performing such analisis. These vector representation can contain all the information from the original barcode, e.g. persistence landscapes, or just a part of it, e.g. Betti curves. The possible tradeoffs between the carried information, complexity, interpretability and interaction with the analysis methods lead to interesting research problems.

Univariate statistical tests

Many times in science, and specially in biology or medicine, we only have a data set of limited size. When this happens, the most common data analysis methods do not apply, and we cannot even assume our values to follow a concrete statistical distribution. In such case, univariate non-paramteric statistical tests, like the Mann–Whitney U test, are a commonly used. In order to study barcodes using these tests, we need to summarize their information with just a number.

Persistent entropy

Persistent entropy is an example of a function that can be used to obtain a number from a barcode. It can be seen as the Shannon entropy of the lenght of the bars, and was first introduced in [CGGJK-2015] and [RCMP-2016]. In the paper [AGS-2020], we studied its formal properties and proposed how to combine persistent entropy and the betti curve to create a new vectorization method, the entropy summary function. There exists implementations of persistent entropy in gudhi and persim. I made a tutorial for gudhi about how to use persistent entropy in TDA.

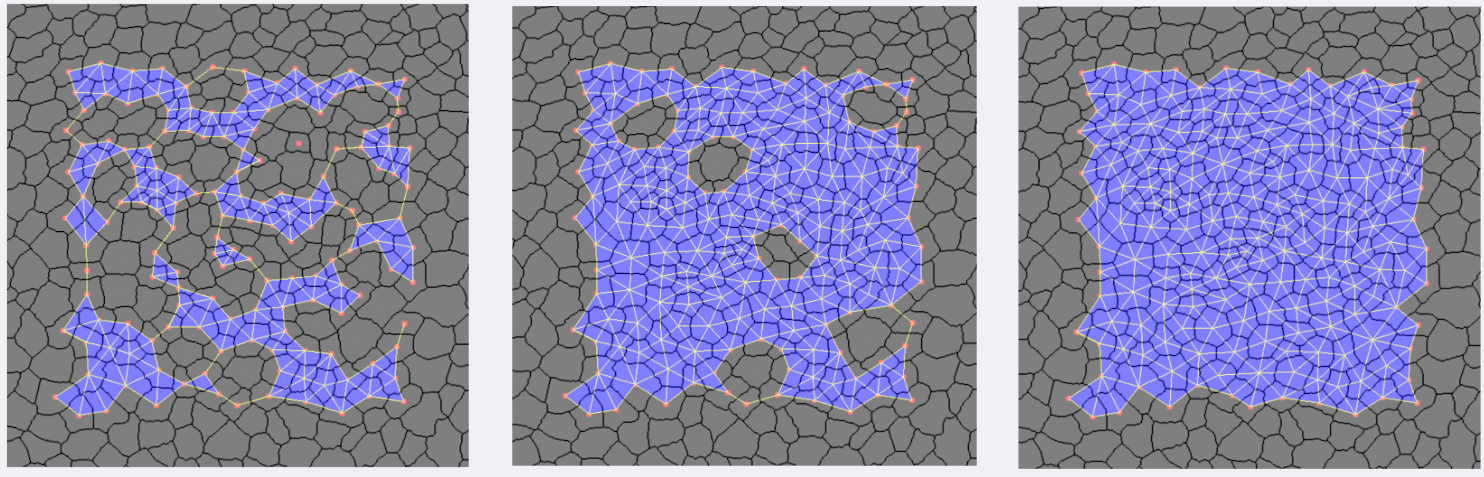
Application to epithelial tissues

We were also interested in studying if TDA could measure the differences between the geometrical and topological organization of planar epithelial tissues. The available data set was small, between 12 and 20 images per type of tissue so it seemed the right settings for using univariate statistical tests. For this studied, we considered numbers obtained from persistent entropy, evaluation of tropical polynomials and the norm of persistence landscapes. We also used different filtrations based in the contact network of the cells and the relative positions of their centroids. The results were showed in our publication [AJS-2021].

TDA in machine learning

There are different ways TDA can contribute to machine learning tasks [AAJNPS-2024]. One of them, if to use TDA to quantify some geometrical/topological aspects of the data set and use the resulting vectors as inputs for machine learning algorithms. As we explained before, there are many possible vectorization methods. The aim of our research was to compare a big collection of them in classiffication tasks of different classical data sets. The results were very surprising, vectors formed by list of numbers obtained from simple methods like mean, variance or persistent entropy were performing better than more sofisticated methods. The whole analysis can be found in [AAJNPS-2024]

Conclusions

One the conclusions obtained from these papers is that simple statistics, like length of the bars, percentiles of the birth/deaths or persistent entropy, have been understimated by the literature. A combination of them may outperform other vectoriations method as seen in [AAJNPS-2024]. In particular, as seen in [AJS-2021] unvariate statistical variables can help to quantify geometrical or topological features when the size of the studied data set is small, and depending on the nature of the studied data set, can also be robust to noise [AJS-2021, AGS-2020].

References

[MMH-2011] Y. Mileyko, S. Mukherjee, J. Harer. Probability measures on the space of persistence diagrams. Inverse Problems 12. 2011

[CGGJK-2015] H. Chintakunta, T. Gentimis, R. Gonzalez-Diaz, M.J. Jimenez, H. Krim. An entropy-based persistence barcode. Pattern Recognition 48-2. 2015

[BPCM-2016] M. Rucco, F. Castiglione, E. Merelli, M. Pettini. Characterisation of the Idiotypic Immune Network Through Persistent Entropy. Proceedings of ECCS 2014, Springer International Publishing. 2016.

[AGS-2020] N. Atienza, R. González-Díaz, M. Soriano-Trigueros. On the stability of persistent entropy and new summary functions for topological data analysis. Pattern Recognition, 107, 107509. 2020.

[AJS-2021] N. Atienza, M.J. Jimenez, M. Soriano-Trigueros. Stable topological summaries for analyzing the organization of cells in a packed tissue. Mathematics, 9(15), 1723. 2021.

[ZKNHRP-2023] A.Zia, A. Khamis, J. Nichols, Z. Hayder, V. Rolland, L. Petersson. Topological Deep Learning: A Review of an Emerging Paradigm. arXiv:2302.03836, aug 2023.

[AAJNPS-2024] D. Ali, A. Asaad, M.J. Jimenez, V. Nanda, E. Paluzo-Hidalgo, M. Soriano-Trigueros. A survey of vectorization methods in topological data analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2023.